Co-Information

The co-information [Bel03] is one generalization of the Mutual Information to multiple variables. The co-information quantifies the amount of infomration that all variables participate in. It is defined via an inclusion/exclusion sum:

\[\begin{split}\I{X_{0:n}} &= -\sum_{y \in \mathcal{P}(\{0..n\})} (-1)^{|y|} \H{X_y} \\ &= \sum_{x_{0:n} \in X_{0:n}} p(x_{0:n}) \log_2 \prod_{y \in \mathcal{P}(\{0..n\})} p(y)^{(-1)^{|y|}}\end{split}\]

It is clear that the co-information measures the “center-most” atom of the diagram only, which is the only atom to which every variable contributes. To exemplifying this, consider “giant bit” distributions:

In [1]: from dit import Distribution as D

In [2]: from dit.multivariate import coinformation as I

In [3]: [ I(D(['0'*n, '1'*n], [1/2, 1/2])) for n in range(2, 6) ]
Out[3]: [1.0, 1.0, 1.0, 1.0]

This verifies intuition that the entire one bit of the distribution’s entropy is condensed in a single atom. One notable property of the co-information is that for \(n \geq 3\) it can be negative. For example:

In [4]: from dit.example_dists import Xor

In [5]: d = Xor()

In [6]: I(d)
Out[6]: -1.0

Based on these two examples one might get the impression that the co-information is positive for “redundant” distributions and negative for “synergistic” distributions. This however is not true — consider the four-variable parity distribution:

In [7]: from dit.example_dists import n_mod_m

In [8]: d = n_mod_m(4, 2)

In [9]: I(d)
Out[9]: 1.0

Meaning that the co-information is positive for both the most redundant distribution, the giant bit, and the most synergistic, the parity. Therefore the coinformation can not be used to measure redundancy or synergy.

Note

Correctly measuring redundancy and synergy is an ongoing problem. See [Griffith2013] and references therein for the current status of the problem.

Visualization

The co-information can be visuallized on an i-diagram as below, where only the centermost atom is shaded:

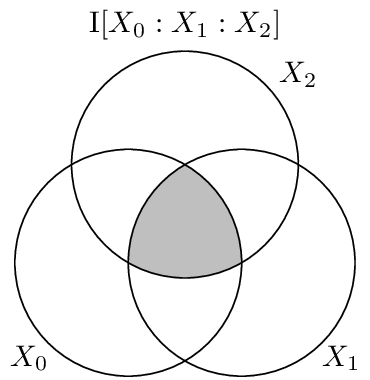
The co-information :math:`\I{X : Y : Z}`

API

coinformation(*args, **kwargs)[source]

Calculates the coinformation.

Parameters:
  • dist (Distribution) – The distribution from which the coinformation is calculated.
  • rvs (list, None) – The indexes of the random variable used to calculate the coinformation between. If None, then the coinformation is calculated over all random variables.
  • crvs (list, None) – The indexes of the random variables to condition on. If None, then no variables are condition on.
  • rv_mode (str, None) – Specifies how to interpret rvs and crvs. Valid options are: {‘indices’, ‘names’}. If equal to ‘indices’, then the elements of crvs and rvs are interpreted as random variable indices. If equal to ‘names’, the the elements are interpreted as random variable names. If None, then the value of dist._rv_mode is consulted, which defaults to ‘indices’.
Returns:

I – The coinformation.
Return type:

float
Raises:

ditException – Raised if dist is not a joint distribution or if rvs or crvs contain non-existant random variables.

Examples

Let’s construct a 3-variable distribution for the XOR logic gate and name the random variables X, Y, and Z.

>>> d = dit.example_dists.Xor()
>>> d.set_rv_names(['X', 'Y', 'Z'])

To calculate coinformations, recall that rvs specifies which groups of random variables are involved. For example, the 3-way mutual information I[X:Y:Z] is calculated as:

>>> dit.multivariate.coinformation(d, ['X', 'Y', 'Z'])
-1.0

It is a quirk of strings that each element of a string is also an iterable. So an equivalent way to calculate the 3-way mutual information I[X:Y:Z] is:

>>> dit.multivariate.coinformation(d, 'XYZ')
-1.0

The reason this works is that list(‘XYZ’) == [‘X’, ‘Y’, ‘Z’]. If we want to use random variable indexes, we need to have explicit groupings:

>>> dit.multivariate.coinformation(d, [[0], [1], [2]], rv_mode='indexes')
-1.0

To calculate the mutual information I[X, Y : Z], we use explicit groups:

>>> dit.multivariate.coinformation(d, ['XY', 'Z'])

Using indexes, this looks like:

>>> dit.multivariate.coinformation(d, [[0, 1], [2]], rv_mode='indexes')

The mutual information I[X:Z] is given by:

>>> dit.multivariate.coinformation(d, 'XZ')
0.0

Equivalently,

>>> dit.multivariate.coinformation(d, ['X', 'Z'])
0.0

Using indexes, this becomes:

>>> dit.multivariate.coinformation(d, [[0], [2]])
0.0

Conditional mutual informations can be calculated by passing in the conditional random variables. The conditional entropy I[X:Y|Z] is:

>>> dit.multivariate.coinformation(d, 'XY', 'Z')
1.0

Using indexes, this becomes:

>>> rvs = [[0], [1]]
>>> crvs = [[2]] # broken
>>> dit.multivariate.coinformation(d, rvs, crvs, rv_mode='indexes')
1.0

For the conditional random variables, groupings have no effect, so you can also obtain this as:

>>> rvs = [[0], [1]]
>>> crvs = [2]
>>> dit.multivariate.coinformation(d, rvs, crvs, rv_mode='indexes')
1.0

Finally, note that entropy can also be calculated. The entropy H[Z|XY] is obtained as:

>>> rvs = [[2]]
>>> crvs = [[0], [1]] # broken
>>> dit.multivariate.coinformation(d, rvs, crvs, rv_mode='indexes')
0.0

>>> crvs = [[0, 1]] # broken
>>> dit.multivariate.coinformation(d, rvs, crvs, rv_mode='indexes')
0.0

>>> crvs = [0, 1]
>>> dit.multivariate.coinformation(d, rvs, crvs, rv_mode='indexes')
0.0

>>> rvs = 'Z'
>>> crvs = 'XY'
>>> dit.multivariate.coinformation(d, rvs, crvs, rv_mode='indexes')
0.0

Note that [[0], [1]] says to condition on two groups. But conditioning is a flat operation and doesn’t respect the groups, so it is equal to a single group of 2 random variables: [[0, 1]]. With random variable names ‘XY’ is acceptable because list(‘XY’) = [‘X’, ‘Y’], which is species two singleton groups. By the previous argument, this is will be treated the same as [‘XY’].